Power factor is one of those subjects about which there seems to be a great deal of confusion and many misconceptions. The culprit is the the assertion that power factor = cos(Φ), Φ (Phi) being the phase shift between voltage and current. While this is true under certain ideal conditions, there are many real-world instances where it is quite incorrect. This article will give you a basic introduction into power factor, and explain why cos(Φ) is not the whole answer.
SPLat Controls specialise in designing and making board level embedded programmable controller products for Original Equipment Manufacturers. So if you make a product that needs intelligent controls, please head on over to our main site and see how a SPLat controller can give you an unfair advantage!
The Basics
If you connect a sinusoidal voltage source to a resistor, current will flow,
power will be dissipated in the resistor and the resistor will heat up. The
current is given by I = V ÷ R and the power is given
by P = I × V or
P = V² ÷ R. The voltage and current are the
rms values.
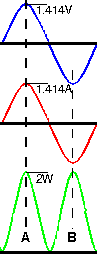
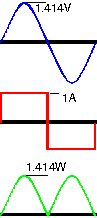
Figure 1 shows the waveforms for this experiment. The top blue waveform is sinusoidal voltage. The voltage is 1V rms giving a peak voltage of 1.414V, The red waveform is the current. It is 1A rms, 1.414A peak. (If you are awake you will deduce that the resistor is 1Ω). The green waveform is the instantaneous power, i.e. the product of voltage and current from moment to moment. For example, at the lefthand vertical line the voltage and current are both at their peaks, so the power is
1.414V × 1.414A = 2W
At the righthand vertical line we are at the negative peaks of voltage and current. Here the instantaneous power is
-1.414V × -1.414A = 2W
i.e. the product of two negatives giving a positive. It should not take too much imagination to see that the average of the power waveform is 1W.
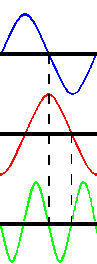
Suppose we now replace the resistor with an inductor. The current in an
inductor lags exactly 90° behind the applied voltage (at least for a perfect
inductor, which we assume we have). This is illustrated by the red current
waveform in figure 2. Now look at the instantaneous power waveform. Between the
vertical lines we have a negative voltage being multiplied by a positive
current, giving a negative power. Negative Power!?
What does that mean?
What the negative power means is that during that part of the cycle, energy is actually transferred from the inductor (load) back into the voltage source. An inductor is an energy storage device. The energy stored in an inductor is ½I²L.
If the load is a perfect inductor the negative power will exactly cancel the positive power, and we get a net power dissipation of zero. However, the voltage is still 1V and the current is still 1A, giving a product which is definitely not zero. Our supposed 1W of input is not producing 1W of heat. This is commonly called "wattless watts". The correct term is Volt-Amps or VA. We say the circuit is drawing 1VA but consuming no power.
The ratio between power and VA is power factor
The pure inductor dissipates no heat, so it has a power factor of zero.
Imagine now that we use an inductor and a resistor simultaneously, connected
in parallel with each other. (this whole argument can be developed with them in
series, but parallel connection is easier to visualise).
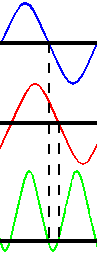
The same voltage as before has been applied to both inductor and resistor. Hence, each one must be drawing the same current as before, with the resistor drawing 1A in phase with the supply voltage and the inductor drawing 1A at a phase lagging the voltage by 90°. The overall current (Fig 3) is the moment to moment summation of these two currents. It can be shown graphically or mathematically that the total current has a phase exactly half way between the two individual currents (i.e. lagging the voltage by 45°) and a magnitude of 1.414A (for unequal component currents the composite is the hypothenuse of a right angle triangle drawn with the lengths of the two other sides equal to the two components).
So, where does this leave us with our power factor calculation? The input voltage is 1V and the current 1.414A, so the input VA is 1.414VA. The power consumed is 1W, the same as in the resistor-only case. Hence, the power factor is 1W ÷ 1.414VA = 0.707. It just so happens that the cosine of the phase angle (Φ) between voltage and current is also 0.707 (cos45°=0.707). This is informal proof of the generally accepted assertion that PF = Cos(Φ). We will now show that that is not always the case.
It ain't necessarily so!
Imagine now that we make a load which always draws exactly ±1A, with the same polarity as the voltage but with a magnitude independent of the voltage. (How make such a load is merely an engineering problem.) With this load the voltage is 1V RMS, and the current is 1A RMS, giving an input of 1VA. The average power in the green waveform is 0.9W (1.414 × 2 ÷ pi). And yet, there is no negative power (the load cannot store power and return it to the supply like an inductor can) and the load current is seemingly in phase with the voltage. The power factor of this circuit is 0.9, yet there is no phase shift. What gives?!
The answer lies in the shape of the current waveform, which in this instance is a square wave. A square wave can be shown to be the summation of a whole number of waveforms at different frequencies, each frequency being a multiple of the fundamental. (If this is unfamiliar to you, you can download a spreadsheet which illustrates the generation of a squarewave as the summation of many sinewaves. This ZIP file unzips to an Excel .xls file. harmonic.zip (14kB). It can be shown that in a squarewave with amplitude 1V (2Vpp) the amplitude of the fundamental frequency is 0.9V. Hence where harmonics are present in the load current (but not in the voltage) the harmonic currents contribute nothing to the power in the load but do reduce the power factor. Is such a situation likely to occur in the real world? Yes it is. In fact, the only loads on the mains which are not likely to introduce harmonic currents are purely resistive loads such as heaters and incandescent lamps.
Power Factor Instruments
An important consequence of the realization that cos(Φ) and PF are not synonymous is in instrumentation, i.e. how we measure power factor. In the power industry power factor meters are quite common. The misconception about cos(Φ) goes so far that many meters are actually labelled "cos(Φ)", perhaps because it looks more technical than Power Factor. Many very expensive instruments have absolutely nothing in their specifications to define exactly what it is they measure. Imagine: An instrument could be designed which merely measures the phase angle using zero crossing detectors. This could be labelled cos(Φ) and sold for a lot of money. We don't know if this has ever been done, but would not be surprised to discover that it had. Do not trust an instrument if you don't know exactly what it measures. One excellent instrument is the Fluke Model 40 (we are not in any way associated with Fluke, but have used the Model 40). This instrument is for use on mains circuits at 110V and 240V 50/60Hz. It has a voltage input and a current clamp. Internally it uses a DSP chip and carefully synchronized dual A to D converters to analyse the voltage and current waveforms. It displays harmonics of current and voltage up to 31st harmonic. Fluke define two separate power factor measurements: Displacement Power Factor (DPF) and plain Power Factor (PF). DPF is the cosine of the phase angle between the fundamental frequency components of voltage and current. The Model 40 actually mathematically extracts the fundamental waveforms from the inputs and then measures the phase angle between them. In the Model 40, PF is the true ratio between VA and power with all harmonics factored in.
We are aware that other instruments exist which are equally correct in their operation, and will list them if brought to our attention. One such instrument is a setup we made ourselves with a PC plug-in A to D card and some custom designed input circuitry. Our results correlate very well to the Fluke Model 40, giving a good feeling of confidence in both.
Power factor, consumer electricity costs, and scams
In recent years a number of products have been offered online that claim to reduce domestic electricity bills by up to 10%-20% by correcting the overall power factor of a private home. These are scams. Domestic electricity users are billed only for real power (watts) not VA because that's all domestic power meters can measure.
The facts on power factor versus domestic electricity bills are documented in an article Power Factor Correction - Scam Review at open4energy.com. They also have a comprehensive Directory of Energy Scams. If you genuinely want to save electricity, look at their page Smart Ways to Save Electricity. Open4Energy.com is an open source publisher of energy monitoring and energy saving solutions. They promote open source software applications, publish FREE information, host discussions and provide audit and consulting services on the demand side energy management. Whether you are an IT professional, a facilities manager, or a home owner, open4energy has software and knowledge which will help you save energy.
The United States National Institute of Standards and Technology (NIST) has released an authoritative report on cost savings due to power factor reduction. This explains why home-owners in the USA will not save money by installing power factor correction devices.