PID implementation: Tuning

At last, we have PIDassist set up to model the characteristics of our target process as closely as we can, and we are ready to start simulating a PID controller acting on that system. The object now is to find the controller settings that give the best control performance as well as a robust solution. Robust means that the control still works OK if the process changes (within reason). Process changes may be a result of wear, different loading, raw material differences, different mains voltages etc.

The technique of adjusting the settings of a controller is called 'tuning'. There's a very large body of experience around on tuning PID loops with linear characteristics, including some very neatly encapsulated sets of rules that make the job pretty easy in most cases. We'll be using one of the most common approaches, referred to as 'Ziegler-Nichols'. I've included web references to a few of others in case you're keen and energetic enough to try them. They use various testing approaches, and produce slightly different results.

The tuning information that follows is for 'linear' systems. Specifically, it is less applicable for control schemes that use 1-bit (bang bang) control. Some of the general principles still apply, but system behaviour under bang-bang control will probably differ from what's described here. With a bit of luck, if your system and controller are linear, the rules in this section will work pretty well. If you controller is bang-bang you can still follow them, but you may have to experiment to a greater degree.

Here are general guidelines that it helps to be aware of.

• Higher values of Ap and Td correspond to 'more' of the associated action being applied.
• A LOWER value of Ti corresponds to 'more' integral action being applied. (yes, a bit confusing, but that's the standard approach!)
• Too much of any of these control actions will probably cause the system to oscillate. This is a condition that must be avoided at all times.
• As Ap increases in the absence of integral action, offset decreases but the system tends towards oscillation. As Ap decreases, control quality degrades.
• Derivative generally works only within a fairly narrow range of settings. Too little (Td too low): no effect, too much (Td too high) system tends towards oscillation.
• Too little integral (Ti too high): offsets reduce too slowly or not at all. Too much (Ti too low), system tends towards oscillation.

On the subject of derivative... Derivative may well not be needed in your controller, and there are significant advantages in leaving it out. The hierarchy in control modes goes something like this:

• If you only use proportional action (Ti very large or integral explicitly disabled by some means, Td = 0), then your controller will probably 'work' after a fashion, but will most likely settle with an unacceptable persistent offset between the target and actual values. If the dynamics of the process are such that you can run with a fairly high gain, you may not need any integral at all (but this is rather unlikely).
• If you use proportional + integral (Td = 0), then you could well find your controller thoroughly acceptable for your application. You only have 2 adjustments to make, and they are relatively easy (easier than derivative) to set up. The control response may not be quite as fast as it can be made, but this may not be a problem.
• If you use all 3 control terms, the potential exists to tune the controller for the best possible response that conventional PID can offer. This may not be a great deal faster than you can achieve without derivative. The penalty you will pay is greater complexity in setting up, and possibly a greater risk of unexpected system instability if your system characteristics change over time.

With occasional exceptions, derivative should not be used:

• On systems with effectively only one time constant.
• On level controls.
• On systems with noisy measurements.

On this question of whether to use derivative or not, well over 80% of the controllers used in major process plants do not use derivative, and don't suffer significantly in consequence.

Start with the following settings, which will result in almost total lack of control;

1. Horizontal time scale about 0.5 times the longest time constant in the process.
2. Controller Ap = 1/Process Gain * 0.1 (effectively a very low gain)
3. Controller Ti = 0 (PIDassist disables integral action if Ti=0)
4. Controller Td = 0
5. Sampling time Ts = ideally, less than 1/10 of the shortest time constant in the system. If the system has more than two time constants, this can be stretched a bit, ½ to 1/3 the fastest time constant may be OK.
6. High and low setpoint values that should give about 20% and 80% of the available range of outputs. What those values are depends on the gain and output offset of the process.
7. Input quantisation off and output quantisation set to infinite resolution. I think it's best to not clutter the picture initially with quantisation noise.
8. If your are going to be using an MMi200 or SL99 analog output, enable the output PWM filter.

Uncheck the Closed Loop check box and start the simulation ("un-pause"). Note that the Pause button is automatically activated each time you click on many of the parameter fields.

Now it's time to get going. The principle of this tuning approach, known as "Ziegler-Nichols Continuous Cycling Method" is to deliberately set the process, or its simulation, gently oscillating. The characteristics of the oscillation are measured and used to calculate the appropriate settings for Ap, Ti and Td. Proceed as follows:

Increase the gain progressively, applying a small step in setpoint every time. Until you start to see a bit of overshoot, doubling the gain is a reasonable approach. Once the response starts to liven up, make the gain increments smaller, until a time will come when you will get a nice, steady ongoing swinging. Here are few typical displays as you approach this condition:

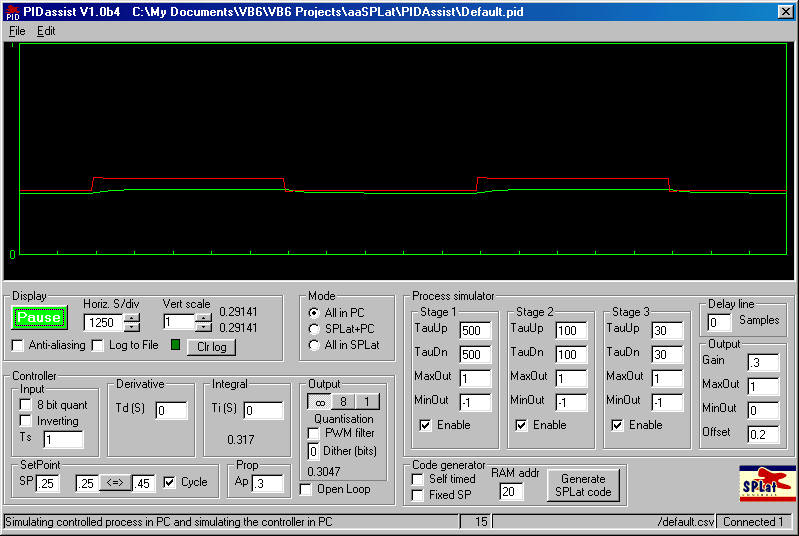
The display above is with the initial suggested settings. On the next several illustrations the gain is slowly increased to, and beyond the point of steady oscillation

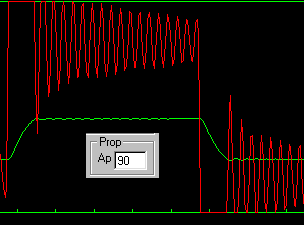
At this stage (once there is some oscillation) I turn off the the setpoint cycling (uncheck the cycle checkbox) and fine tune the gain until I find a setting that gives a steady oscillation that is not saturating the red controller output plot.

Note that at this stage, your controller is using only proportional action. If you apply integral or derivative now it will confuse the situation totally.

If your oscillation starts to increase it means that your gain is too high, and if you keep going the amplitude will increase until something limits it. So watch your testing carefully and be prepared to immediately reduce Ap if you see oscillations growing. With a bit or practice, you can steady the oscillation out at a nice, controlled low level with a couple of deft tweaks of Ap.

With a simulation you can't do any damage if the oscillation gets too big, but with a real device maybe you could. If you're new to this game, I really suggest that you do some tuning on PIDAssist before trying it on a real process (that's what PIDAssist is for!) The simulator is a totally safe environment to teach you the touch that is required to edge the process into a gentle controlled oscillation, then to back it out again to good control. It may give you confidence to know that technicians regularly put giant process units such as catalytic crackers in oil refineries into gentle, controlled oscillation to determine tuning settings. If they can do it, you can too!

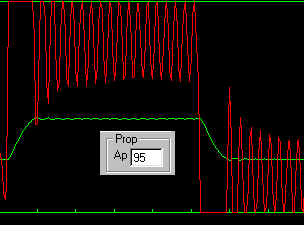
Once you have your steady oscillation, make a note of the following 'test' variables. For the period, an 'eyeball' approximation (+/- 10%) will do:

Value of Ap, referred to here as Apt

Value of the oscillation PERIOD, referred to here as Pt. This is the time between two consecutive up (or down) peaks, as in the following diagram (I've altered the display time scale to stretch out the period on the screen):

We have about 2.5 horizontal divisions at 125S/div, so Pt = 2.5 * 125 = 312.5S (Hint: For better accuracy measure the period of 5 cycles then divide by 5.

You are now pretty close to done! The next step is to calculate the values for the 3 tuning parameters that, hopefully, will give you a good response. These values are as follows, depending on whether you plan to use Derivative or not:

	Derivative not included	Derivative included
Ap	Apt * 0.45	Apt * 0.6
Ti	Pt / 1.2	Pt / 2
Td	-	Pt / 8

You now just enter these settings into your controller, and apply another step. If everything is going to plan, what you should see is something like this:

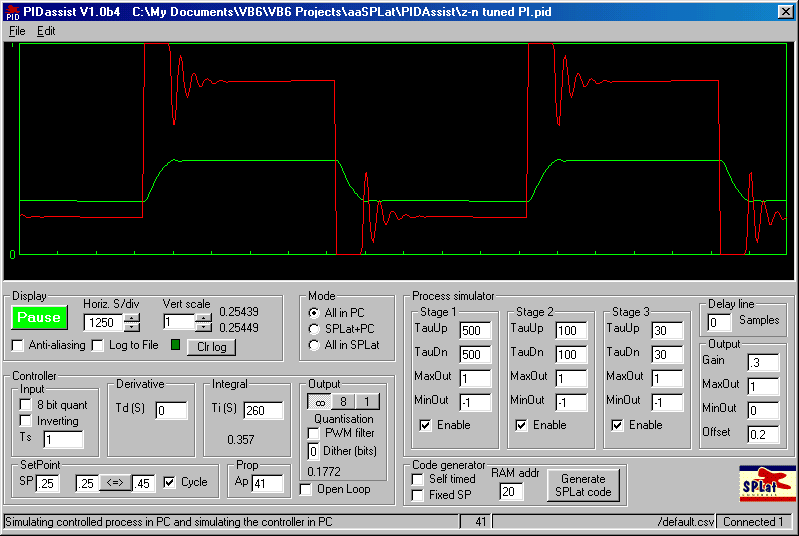
The above diagram is the tuning result without derivative action. The one below has the settings with derivative action.

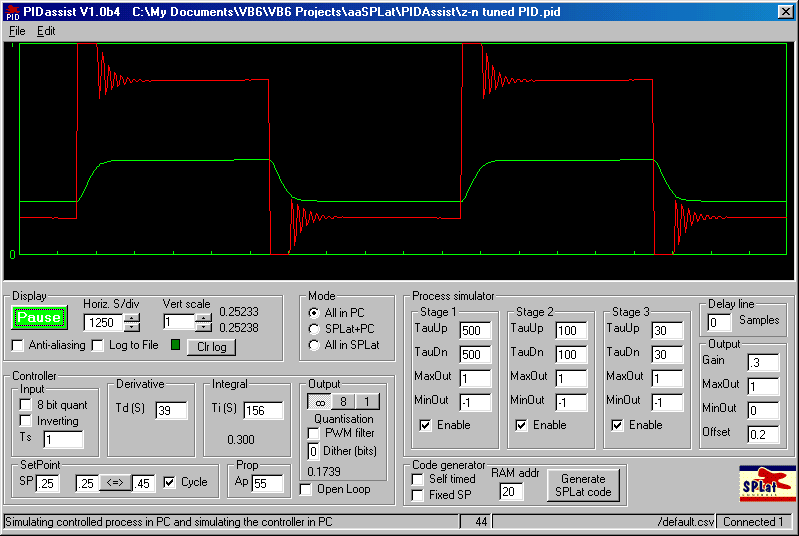
From the perspective of formal 'tuning', that's it. It's taken a while to explain, but once you get the hang of it you'll find it's easy. Of course if your process has time constants of hours, it will take that long on the real process :-). One other reason to get serious about PIDAssist.

Now that you've achieved a reasonably acceptable response, your next step is to do some 'seat of the pants' tweaking. It's common to reduce the gain (Ap) by maybe 10 - 20% to increase the margin between normal operation and potential instability.

During testing, you'll find the undo function in PIDAssist useful in backing out of unsuccessful test runs quickly.

Watch the actual numerical output values in the display pane (raw top, filtered below). It sometimes happens that the output response looks beautiful, but the actual values are wrong. That can happen especially if the controller output is saturating.

Once you have established parameters that give a good result, you need to look at input and output quantisation.

If you are using an analog input on the SPLat, turn on input quantisation. This may very well result in more noise, especially in the red controller output. Some noise will do no harm (unless maybe you are using an electromechanical relay as a driver, in which case you will want to minimise plain old mechanical wear). However, if the output saturates a lot the noise can produce a rectification effect and result in a shift in the average process output (so watch it!).

You will almost certainly need to test output quantisation. Pick the output settings that best match your application.

Finally you need to test your settings for robustness. That means you check that for all likely changes in the process parameters such a gain and major and minor time constants the control system will continue to perform acceptably. This will involve some careful thinking about and analysis of your process. For example, ±10% variation in mains voltage applied to a heater will produce ±20% variation in heater power, which would translate directly into similar gain changes. Think differently about normal and abnormal changes. Your system should stay within its specs for normal variations. For abnormal variations, beyond what it is specified to work with, you should at least aim for graceful and hazard-free degradation. In that analysis include possible silly things an end-user might do to your system. That is where integrating the logic control aspects of SPLat into the PID control may come into play.

When you are happy with the simulation results, save the configuration (*.pid) file. It is precious!