PID theory: Asymmetrical time constants

There are systems that clearly move more quickly in one direction than the other. However, you need to be careful with this one, in many cases the cause of this asymmetrical behaviour is not what it seems to be. As an example, consider our kettle. With the heat on, the temperature increased quickly, but with it off it dropped a lot slower. Your first reaction might be to say: "well, there are obviously two time constants at work here, one for heating and the other for cooling". NOT SO. Neglecting various secondary effects, there is one time constant at work all the time. The different rates that we observe are due to the different "forcing functions" that are in play. During heating we have an electric element producing maybe 500 watts, and during cooling we have a loss of heat to the environment, maybe 30 watts. That's what causes the heating to be fast, and the cooling slow. If you arranged for the cooling heat removal to be 500 watts, for example by putting the poor kettle into iced water (or liquid nitrogen if necessary), you'd find, of course, that the temperature dropped just as fast as it went up.

This distinction is not just semantics. If you assumed a system model for your kettle with 2 time constants based on the measured temperature change rates, and did a continuous PID control design on that basis, you could well end up with a control system that failed to work. So you can see how it can be tricky to define the characteristics of real world systems.

Genuine 2-time constant - one when ascending, one when descending - systems do exist. Their essential characteristic is difference in response times for up and down directions for forcing functions of opposite sign but SAME MAGNITUDE. If you suspect this behaviour, you should look for an explicit mechanism – such as check valves, diodes or similar devices with asymmetrical behavior. If you can't see any mechanism of this sort, look very carefully at the situation and see if you're being tricked as with the kettle example. Control design can be an intriguing business!

The asymmetrical time constant capability within PIDAssist allows that configuration to be modelled if it is encountered.

The spreadsheet "assymetricTC.xls" lets you explore asymmetrical time constants. It has the same 3 columns as multipleTC.xls, but each column has two K factors, one for going up and one for going down. The initial values are:

The input is set initially to alternate between 1 and 0 and back again every 200 steps. The resultant outputs look like the adjacent graph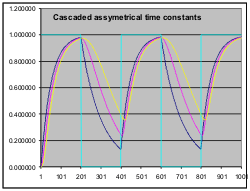

The PIDassist program allows you to simulate up to 3 cascaded asymmetrical time constants.

In electronic terms an asymmetrical time constant could be approximated with a capacitor, two series resistors and a diode connected across one of the resistors.